Across the Whole Board
Across the Whole Board
I. Drawing the Network
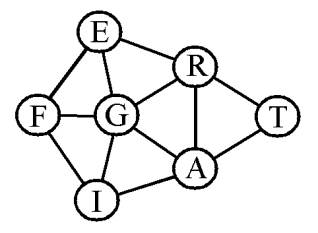
From the start of the game until such time as one Great Power is knocked out of contention (at which point the network changes), almost every war that takes place will occur along one of the twelve lines on the diagram, and almost every agreement will be aimed at preventing a war along one of the twelve lines of the diagram (fig. 1).
Fig. 1
II. Relation between Strength of Country and Number of Neighbours
As Diplomacy progressed from its initial form to its final market form, it was played frequently by a group of good players who steadily progressed in their understanding of the game against steadily improving opponents. The strength of the countries as determined by experience within this group ran from Turkey at the strongest down through Britain, France, Italy, Russia, Austria-Hungary, and lastly, Germany. We note the close correspondence of that list to the list of countries in reverse order of the number of neighbours, as read off the network: Turkey, 2; England, France and Italy, 3; Russia and Austria-Hungary, 4; Germany 5.
III. An Aside concerning Strength of Countries
The relative strength of countries in postal play had generally followed the pattern given above, except for the single major anomaly that Russia was considered to be the strongest country. Her apparent strength diminished as that of the more defensively placed countries increased as the players gained experience.
Recent careful analysis has revealed a satisfactory opening variation for Italy against Turkey, called the Lepanto Opening. The remarks in the first part of this article assume that that opening is not being used. Later in this article we will describe and discuss the Lepanto Opening directly.
IV. Certain Alliances Schematized on the Network
Germany and Russia frequently lead off by forming an alliance in which both agree to refrain from moving to the Baltic Sea, Livonia, Prussia or Silesia. Russia may demand, and Germany may agree to permit, Russia entry into Sweden in Fall 1901 as part of this alliance. Germany may threaten to block that entry unless he gets the alliance. Germany and Austria-Hungary also frequently agree to refrain from moving to Silesia, Bohemia and Tyrolia.
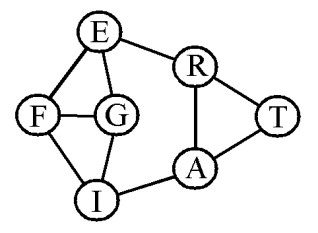
If these agreements are kept, and they usually are (for neutralization agreements work fairly well in this game), then there will be no German-Russian or German-Austrian war in the early stages of the game. Thus we may erase those links from the diagram to see the effect on the whole-board considerations (fig. 2).
Fig. 2.
We now note that six countries each are linked to three neighbours, only Turkey differing in being linked to two. Thus we see the graphic illustration of this writer’s belief that Germany needs two alliances, and Russia and Austria each one, in order to start the game on something like equal footing. This assumes that the other players have not yet made any alliances at all.
In thus modifying the network, it should be pointed out that an alliance is hardly as good as a defensive guarantee as geographic separation, for the alliance may be broken, and also a third party might come through the demilitarized zone sooner or later; but then schematic geographic separation is not ideal either, since it is not a perfect representation of the board.
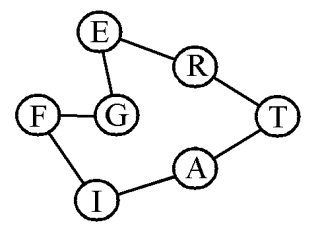
Suppose we ask whether there is a likely alliance structure that can equalize the number of neighbours among all seven countries. There is: if, to the two alliances noted above, we add a Russian-Austrian alliance (neutralizing Galicia at least), and a German-Italian alliance (neutralizing Tyrolia) and an English-French alliance (neutralising the Channel, the Irish Sea and the North Atlantic), then each Power has just two links left on the network (fig. 3).
Fig. 3.
Needless to say, players would still regard one country or another as stronger or weaker, in part because an alliance is not as sure a defence as geographic separation. Suppose, then, that we devised an experimental game in which these alliances were made as binding as geography itself. Suppose we introduced into the experimental game the rule that no pieces could be moved to the aforementioned neutralized zones by any player. Suppose we also rules that no order was valid calling for an attack on a supply centre or province currently occupied by a unit unless the two countries involved were joined by a link in the reduced network shown in our last diagram.
Only after the imposition of those quite restrictive rules would the “number of neighbours” factor be removed from consideration. There would still be differences in strength, due to such factors as sea defences, number of early grabs, rapidity of build-up, and so on. By analysing or actually playing this reduced game, however, the player might help to separate in his mind the pervading number of neighbours consideration from the remainder. This separation might in turn help him to reconstitute the question of relative strength of countries in new situations as they arise.
V. Reverberation Theory
Suppose that after the first move (Spring 1901) has been played, we look around the board and determine apropos of each Power whether its first set of moves has been as expected, better than expected or worse than expected. We also determine whether each Power has been treated as expected by the events of the move, or better, or worse than expected. Our subjective opinion of the whole development for each Power relative to our subjective notion of the expected, may then be entered on the network diagram, alongside that Power’s initial. Usually a simple plus or minus sign is all that can be justified, but double or triple signs may be employed.
Let us suppose for purposes of example that nothing unexpected has happened on the first move, except at one point, at which the development appears to benefit Italy and Austria-Hungary and harm Turkey. The Lepanto Opening might be one such development. Listing the Powers in the first column (see table) we enter +1 or -1 in the second column as appropriate, representing the primary effect. The third column is derived by taking each Power’s figure in the second column, reversing its sign, and awarding it to each of that Power’s neighbours. Thus, if Italy has received a +1 in the second column, each of France, Germany and Austria-Hungary receives a -1 in the third column. Each Power’s receipts in the third column are then added up to form the fourth column.
This process may then be represented as often as one wants: the figures for each country found in the fourth column may be reversed in sign and attributed to all that country’s neighbours, forming a fifth column, with the accumulated partial results in that column added to form the sixth column and so forth.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| England | 0 | +++ | +3 | -3 -2 -3 | -8 | ||
| France | - | -1 | +++ | +3 | -3 -2 -3 | -8 | |
| Germany | - - | -2 | ++ | +2 | -3 -3 -3 -4 -3 | -16 | |
| Italy | +1 | - | -1 | +++ | +3 | -3 -2 -4 | -9 |
| Austria | +1 | - + | 0 | ++++ | +4 | -2 -3 -3 | -8 |
| Russia | - + | 0 | +++ | +3 | -3 -2 -4 | -9 | |
| Turkey | -1 | - | -1 | 0 | -4 -3 | -7 |
The second column shows that Italy and Austria have benefited, and Turkey lost, the result of the subjective appraisal of the position. The fourth column places Austria (0) ahead of Italy (-1), indicating that the event may have benefited Austria more than her ally. The reason is that the country harmed is a neighbour of Austria, but not of Italy. Among the countries not involved in the primary effect, Germany (-2) has lost the most as she neighbours two countries which have benefited; France (-1) neighbours only one country that benefited; England (0) neighbours no country that benefited or lost, and Russia (also 0) neighbours one country that benefited and one that suffered. The sixth column fails to separate England and Russia, but the eighth column indicates that England has done a hair better than Russia, apparently because Austria’s gains pose a greater threat to Russia than to England, while Turkey does not appear quite correspondingly weak, apparently again because of his small number of neighbours.
Thus the greatest benefit from this development apparently accrued to Austria, and less in order to Italy, England, Russia, France, Germany and Turkey. The high standing of England in this list make some wonder whether England should suggest the Lepanto Opening to Italy during the first Diplomacy period, a notion that would never have occurred to me if I had not analysed the matter as shown above. The answer nevertheless is probably no; for other Italian plays such as an early attack on France would score higher for England; and perhaps France should have been awarded a plus at the outset, because the opening turns Italy away from his door, at least for a while. In an ordinary game I would probably also arbitrarily reduce the contribution between Germany and Austria, or eliminate it altogether, when reverberating the first move results; but for the purposes of conveying the principle here we did not want to introduce arbitrary factors, which each user of the tool would introduce for himself.
VI. Diamond Theory
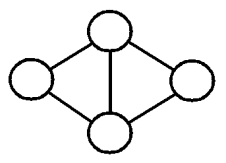
When there are just four countries left in a game, they frequently, though not invariably, neighbour each other in such a way as to form a diamond-shaped diagram (fig. 4).
Fig.4.
We note that the two centre countries have three neighbours each, whereas the two apex countries have only two. Theory would lead us to believe that the apex countries would have the advantage. Naturally, then, as a player lays out his early strategy, and as the possibility of his being left in the Council of Four increases, he wants to jockey himself into an apex position rather than a centre position. Thus we see another reason for the advantage that edge and corner countries have in this game: if they arrive at the Council of Four, they are much more likely to do so as apex countries, than are the centre countries.
It is informative in this regard to turn again to the network of seven countries, and imagine each country eliminated in turn, considering the more likely connectivities to occur across the territory of the defeated, then altering the diagram appropriately; then considering the likelihood of being left on the apex, or the centre, if various successful endeavours are conducted on the six-Power network. Imagining himself playing each Power in turn, the player can postulate sufficient alliances to knock out two of the remaining powers in various combinations, noting that some of these successes may leave him as an Apex Power and others as a Centre Power.
Naturally, then, one would expert alert Centre Powers to attempt to ally with each other to fend off the Apex Powers, and one would expect Apex Powers to act to keep the Centre Powers apart. Centre Powers cannot always keep off each other as they might like to, because the vagaries of the position, including the important division of earth-space into land and sea and of forces into land and sea forces, interferes with theory; and all such interferences tend to favour the Apex Powers.
As Diplomacy players, however, we do not want to rest with a mere all-other-factors-being-equal analysis. The player will wnat to determine in general how important the apex position is in relation to other matters such as number of units. suppose for simplicity that the two Centre Powers are of equal size, and the two Apex Powers are of equal size. Do we tend to arrive at an equal game when the Centre Powers are twice as large as the Apex Powers? Three times? One and a half times? With a workable ratio in mind, the player has more flexibility; he can allow himself to be jockeyed into the centre position if he gets enough advantage in units to compensate. He may know how many units he can offer in his effort to jockey someone else into centre position.
VII. Alliances of Three Countries Not in Contact with All the Other Four
Four countries in alliance ought to be able to defeat the other three, sooner or later, but four-Power alliances are hard to put together and hard to keep together. It can be expected to be easier with three Powers and still easier with two. Indeed, most alliances in most games turn out to be two-Power alliances, and they seldom amalgamate quite completely into four Powers against the other three. (one recalls World War II in which Russia did not go to war against Japan until 1945.) I think that the three-Power alliance has sometimes been underestimated, in particular a three-Power alliance in which there is one Power remaining among the other four Powers who does not border on the allied three can be quite good. Suppose, for example, that England, France and Germany allied with one another, sorted out the small states in their area into appropriate spheres of influence, set up sufficient neutralized zones, and began pressing outwards against Russia, Austria-Hungary and Italy. Sooner or later one would expect, in the worst case, a wall of resistance to form among those three. What, then, would Turkey do? Turkey's mere physical presence in the rear of Russia-Austria-Italy is a serious detriment to them, which is not matched by anything in the rear of England-France-Germany. Thus, in most cases, Turkey will find herself thrown in automatically with the original three. The result is a four to three alliance structure, but one in which the side containing four members has actually had the burden of negotiating among only three.
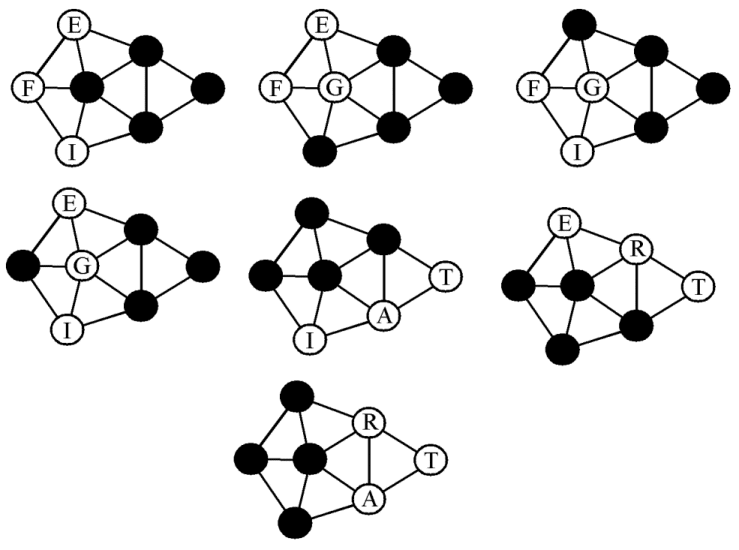
The network diagram makes it easy to determine the few cases in which such three-Power alliances may be formed. Out of 35 possible three-power alliances drawn from a population of seven countries, just seven will be such that the three countries are not in contact with all the other four (Fig. 5).
Fig. 5.
Let us now consider a modification of the network involving the Lepanto Opening. This cleverly calculated opening in a way reminding one of the Hypermodern openings in chess (which appear to contradict principle) calls for Italy to open with A(Ven) hold, A(Rom)-Apu, F(Nap)-ION. He continues with A(Ven) holds, F(ION) C A(Apu)-Tun, build F(Nap). Then, A(Ven) hold, F(ION)-EMS, F(Nap)-ION. Finally, A(Ven) hold, F(ION) & F(EMS) C A(Tun)-Syr. Austria usually rushes into the Balkans, leaving Trieste exposed in order to gain the upper hand against Turkey.
There is also some question whether the Italy-Germany connection is important enough for the network. Italy uses it only rarely and Germany hardly ever. It is something of a matter of choice whether to include it or not - suppose we eliminate it here. Then we find that the diagram taking into account the Lepanto Opening changes as indicated below, and the number of three power alliances which do not neighbour all the other four Powers, is reduced to four (as indicated in Fig. 6.).
Creating an initial three-player alliance seems to work quite well in over-the-board play, but not so well in postal play. Over the board it is easy and fast for three players to talk things over. A group of three contains three different pairs and there is not time in postal play for various proposals and counter-proposals to move up and down the three sides of a triangle.
When the alliance is undertaken in a certain way, however, there is too much time in postal play rather than too little. I experimented recently with planning one of the above three-power alliances on a fair basis for all three, but then arranging it closely with just one of the others, after which we two offered the alliance to the third along with an ultimatum that we would jointly attack him if he refused. In the over-the-board game the alliance was accepted at once and worked out well. There was, however, only a few minutes available to the third man in which to make his decision. When I tried the same thing in postal play, the third man had a couple of weeks in which to brood over the ultimatum, during which he agreed and then refused, protesting the nature of the ultimatum, demanding compensation for his injured feelings, and finally withdrawing from the game, an act which relieved us under the circumstances.
Possibly for better results in the postal game the ultimatum (which should never be called that, or be otherwise offensively worded - it should be moderately worded, but clear) should be sent at such a time that the recipient will have to accept it or reject it within a couple of days.